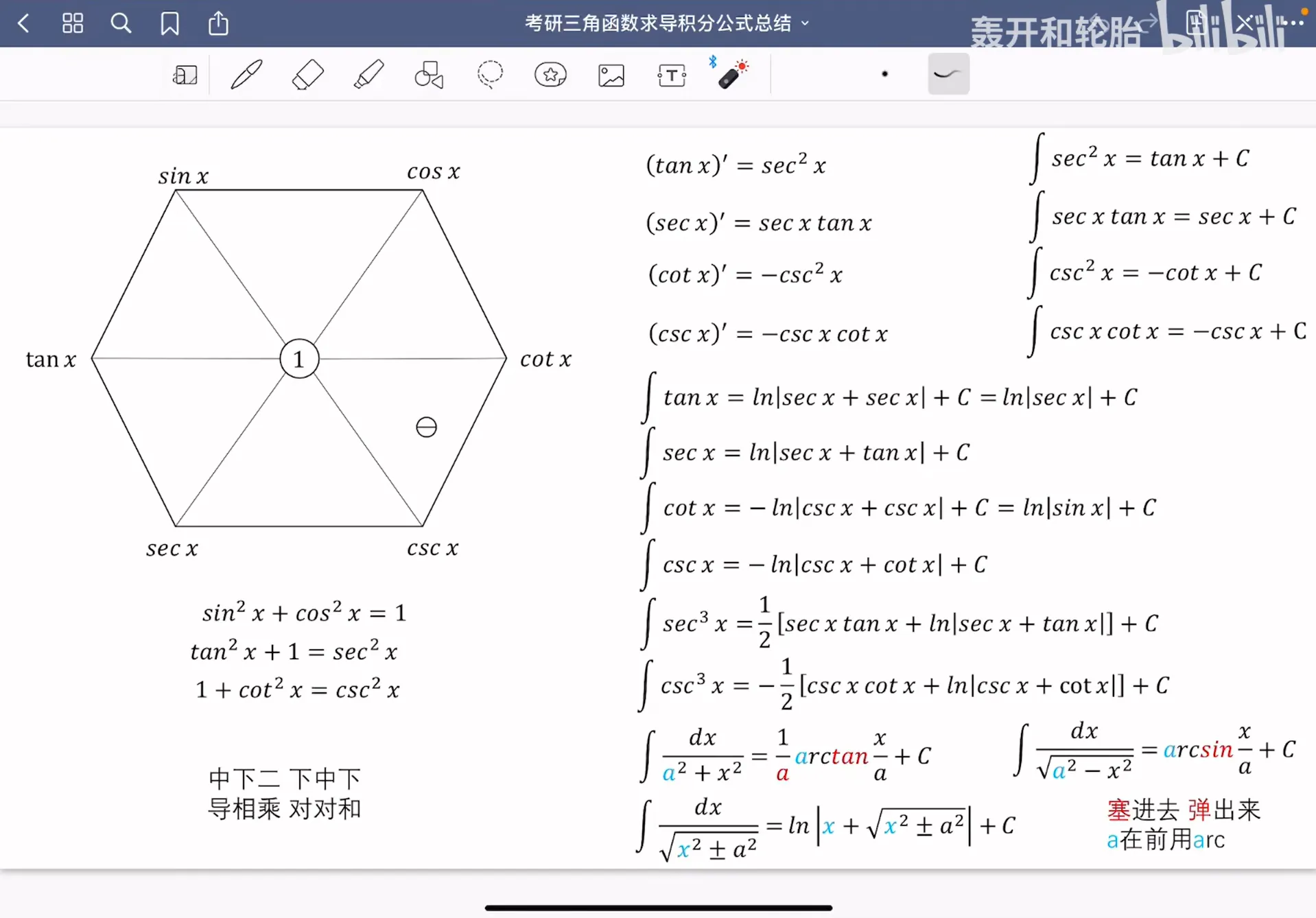
快速记忆

图片来自BV1si4y1R7FG,详细介绍见视频
三角函数
积分
1.\(\int \sin x \, dx = -\cos x + C\)
2.\(\int \cos x \, dx = \sin x + C\)
3.\(\int \tan x \, dx = -\ln|\cos x| + C\)
4.\(\int \cot x \, dx = \ln|\sin x| + C\)
5.\(\int \sec x \, dx = \ln|\sec x + \tan x| + C\)
6.\(\int \csc x \, dx = -\ln|\csc x + \cot x| + C\)
求导
1.\(\frac{d}{dx}(\sin x) = \cos x\)
2.\(\frac{d}{dx}(\cos x) = -\sin x\)
3.\(\frac{d}{dx}(\tan x) = \sec^2 x\)
4.\(\frac{d}{dx}(\cot x) = -\csc^2 x\)
5.\(\frac{d}{dx}(\sec x) = \sec x \tan x\)
6.\(\frac{d}{dx}(\csc x) = -\csc x \cot x\)
恒等变换
基本三角恒等式
- 毕达哥拉斯恒等式:
$$
\sin^2 x + \cos^2 x = 1
$$
$$
1 + \tan^2 x = \sec^2 x
$$
$$
1 + \cot^2 x = \csc^2 x
$$ - 倒数恒等式:
$$
\csc x = \frac{1}{\sin x}
$$
$$
\sec x = \frac{1}{\cos x}
$$
$$
\cot x = \frac{1}{\tan x}
$$ - 商数恒等式:
$$
\tan x = \frac{\sin x}{\cos x}
$$
$$
\cot x = \frac{\cos x}{\sin x}
$$
角度和与差的恒等式
- 正弦的和与差:
$$
\sin(a + b) = \sin a \cos b + \cos a \sin b
$$
$$
\sin(a – b) = \sin a \cos b – \cos a \sin b
$$ - 余弦的和与差:
$$
\cos(a + b) = \cos a \cos b – \sin a \sin b
$$
$$
\cos(a – b) = \cos a \cos b + \sin a \sin b
$$ - 正切的和与差:
$$
\tan(a + b) = \frac{\tan a + \tan b}{1 – \tan a \tan b}
$$
$$
\tan(a – b) = \frac{\tan a – \tan b}{1 + \tan a \tan b}
$$
二倍角恒等式
- 正弦的二倍角:
$$
\sin(2x) = 2 \sin x \cos x
$$ - 余弦的二倍角:
$$
\cos(2x) = \cos^2 x – \sin^2 x = 2 \cos^2 x – 1 = 1 – 2 \sin^2 x
$$ - 正切的二倍角:
$$
\tan(2x) = \frac{2 \tan x}{1 – \tan^2 x}
$$
半角恒等式
- 正弦的半角:
$$
\sin\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1 – \cos x}{2}}
$$ - 余弦的半角:
$$
\cos\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1 + \cos x}{2}}
$$ - 正切的半角:
$$
\tan\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1 – \cos x}{1 + \cos x}} = \frac{\sin x}{1 + \cos x} = \frac{1 – \cos x}{\sin x}
$$
三倍角恒等式
- 正弦的三倍角:
$$
\sin(3x) = 3 \sin x – 4 \sin^3 x
$$ - 余弦的三倍角:
$$
\cos(3x) = 4 \cos^3 x – 3 \cos x
$$ - 正切的三倍角:
$$
\tan(3x) = \frac{3 \tan x – \tan^3 x}{1 – 3 \tan^2 x}
$$
乘积到和的恒等式
- 正弦与余弦的乘积:
$$
\sin a \cos b = \frac{1}{2} [\sin(a + b) + \sin(a – b)]
$$ - 余弦与余弦的乘积:
$$
\cos a \cos b = \frac{1}{2} [\cos(a + b) + \cos(a – b)]
$$ - 正弦与正弦的乘积:
$$
\sin a \sin b = \frac{1}{2} [\cos(a – b) – \cos(a + b)]
$$
和到乘积的恒等式
- 正弦的和与差:
$$
\sin a + \sin b = 2 \sin\left(\frac{a + b}{2}\right) \cos\left(\frac{a – b}{2}\right)
$$
$$
\sin a – \sin b = 2 \cos\left(\frac{a + b}{2}\right) \sin\left(\frac{a – b}{2}\right)
$$ - 余弦的和与差:
$$
\cos a + \cos b = 2 \cos\left(\frac{a + b}{2}\right) \cos\left(\frac{a – b}{2}\right)
$$
$$
\cos a – \cos b = -2 \sin\left(\frac{a + b}{2}\right) \sin\left(\frac{a – b}{2}\right)
$$
反三角函数
积分
1.\(\int \arcsin x \, dx = x \arcsin x + \sqrt{1 – x^2} + C\)
2.\(\int \arccos x \, dx = x \arccos x – \sqrt{1 – x^2} + C\)
3.\(\int \arctan x \, dx = x \arctan x – \frac{1}{2} \ln(1 + x^2) + C\)
4.\(\int \text{arccot } x \, dx = x \text{arccot } x + \frac{1}{2} \ln(1 + x^2) + C\)
5.\(\int \text{arcsec } x \, dx = x \text{arcsec } x – \ln|x + \sqrt{x^2 – 1}| + C\)
6.\(\int \text{arccsc } x \, dx = x \text{arccsc } x + \ln|x + \sqrt{x^2 – 1}| + C\)
求导
1.\(\frac{d}{dx}(\arcsin x) = \frac{1}{\sqrt{1 – x^2}}\)
2.\(\frac{d}{dx}(\arccos x) = -\frac{1}{\sqrt{1 – x^2}}\)
3.\(\frac{d}{dx}(\arctan x) = \frac{1}{1 + x^2}\)
4.\(\frac{d}{dx}(\text{arccot } x) = -\frac{1}{1 + x^2}\)
5.\(\frac{d}{dx}(\text{arcsec } x) = \frac{1}{|x|\sqrt{x^2 – 1}}\)
6.\(\frac{d}{dx}(\text{arccsc } x) = -\frac{1}{|x|\sqrt{x^2 – 1}}\)
恒等变换
基本恒等式
- 反函数关系:
$$
\arcsin x + \arccos x = \frac{\pi}{2}
$$
$$
\arctan x + \text{arccot } x = \frac{\pi}{2}
$$ - 负数参数:
$$
\arcsin(-x) = -\arcsin x
$$
$$
\arccos(-x) = \pi – \arccos x
$$
$$
\arctan(-x) = -\arctan x
$$
$$
\text{arccot }(-x) = \pi – \text{arccot } x
$$
和与差的恒等式
- 反正切的和:
$$
\arctan a + \arctan b = \arctan\left(\frac{a + b}{1 – ab}\right) \quad \text{如果 } ab < 1 $$ $$ \arctan a + \arctan b = \pi + \arctan\left(\frac{a + b}{1 – ab}\right) \quad \text{如果 } ab > 1 \text{ 且 } a, b > 0
$$
$$
\arctan a + \arctan b = -\pi + \arctan\left(\frac{a + b}{1 – ab}\right) \quad \text{如果 } ab > 1 \text{ 且 } a, b < 0
$$ - 反正切的差:
$$
\arctan a – \arctan b = \arctan\left(\frac{a – b}{1 + ab}\right)
$$
反三角函数的其他恒等式
- 与三角函数的关系:
$$
\sin(\arccos x) = \sqrt{1 – x^2}
$$
$$
\cos(\arcsin x) = \sqrt{1 – x^2}
$$
$$
\tan(\arcsin x) = \frac{x}{\sqrt{1 – x^2}}
$$
$$
\tan(\arccos x) = \frac{\sqrt{1 – x^2}}{x}
$$ - 与对数的关系:
$$
\arcsin x = -i \ln\left(ix + \sqrt{1 – x^2}\right)
$$
$$
\arccos x = -i \ln\left(x + i\sqrt{1 – x^2}\right)
$$
$$
\arctan x = \frac{i}{2} \ln\left(\frac{1 – ix}{1 + ix}\right)
$$